La instrucción española de carreteras 5.2-IC de la Dirección General de Carreteras recoge el Método Racional para el cálculo de los caudales máximos, con los que diseñar los drenajes de nuestras carreteras. A continuación se analiza dicha obtención de los caudales de avenida para el diseño de carreteras.
El método racional supone la generación de escorrentía en una determinada cuenca a partir de una intensidad de precipitación uniforme en el tiempo, sobre toda su superficie. Debido a esto, para la aplicación del mismo se debe comprobar que ninguno de estos factores pueda resultar relevante en el cálculo:
- Aportación de caudales procedentes de otras cuencas o trasvases a ellas.
- Existencia de sumideros, aportaciones o vertidos puntuales, singulares.
- Accidentales de cualquier clase.
- Presencia de lagos, embalses o planas inundables que puedan producir efecto laminador o desviar caudales hacia otras cuencas.
- Aportaciones procedentes del deshielo de la nieve u otros meteoros.
- Caudales que afloren en puntos interiores de la cuenca derivados de su régimen hidrogeológico.
De manera general, estas condiciones se cumplen en cuencas cuyo área sea inferior a 50 km2, por lo que se recomienda su empleo en estos casos. Para el resto de escenarios, la Instrucción cita los métodos estadístico e hidrológico como procedimientos más adecuados.
Teniendo en cuenta que, el tiempo de concentración (Tc) puede definirse como el tiempo mínimo necesario desde el comienzo del aguacero para que toda la superficie de la cuenca esté aportando escorrentía en el punto de desagüe. Se puede entender que dicha magnitud depende de la longitud y de la pendiente de la cuenca seleccionada. Esto se materializa en la siguiente expresión, cuya unidad se obtiene en horas al introducir las demás variables en metros:
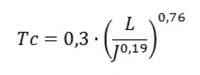
Donde:
- L: es la longitud de la cuenca en km.
- J: es la pendiente de la cuenca en m/m.
En aquellas cuencas principales de pequeño tamaño en las que el tiempo de recorrido en flujo difuso sobre el terreno sea apreciable respecto al tiempo de recorrido total no será de aplicación la fórmula anterior. Deberá consultarse la Instrucción.
La fórmula propuesta permite obtener el caudal de avenida a partir del coeficiente de escorrentía (C), la máxima intensidad media (I) durante el período de cálculo correspondiente al tiempo de concentración Tc, y a partir de la superficie de la cuenca (A) que influirá en el valor del coeficiente de uniformidad (Kt), mediante la expresión:
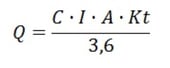
Antes de comenzar a calcular el caudal de diseño, se debe haber obtenido la precipitación máxima diaria de la zona donde se encuentre ubicado el proyecto. Si no se conoce este dato, se puede obtener mediante el cálculo del Ministerio de Fomento, consistente en los siguientes pasos:
1.) Localizar en el mapa de isolíneas, facilitado por el Ministerio de Fomento (Máximas Lluvias diarias en la España Peninsular), el punto geográfico de estudio.
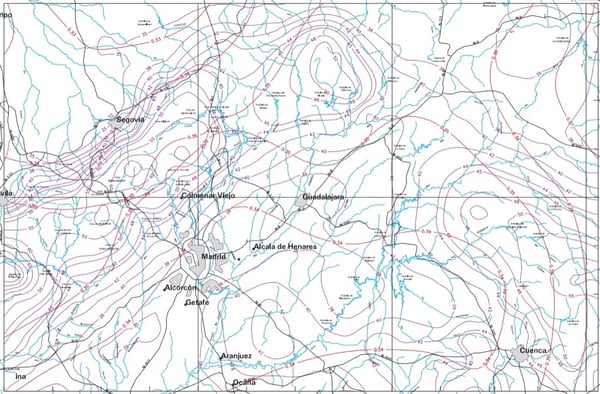
2.) Estimar mediante las isolíneas presentadas el coeficiente de variación (Cv) (líneas rojas con valores inferiores a la unidad) y el valor medio de la máxima precipitación diaria anual (líneas moradas).
3.) Para el periodo de retorno deseado (T) y el valor de Cv, obtener el factor de amplificación (KT) mediante el uso de la siguiente tabla.
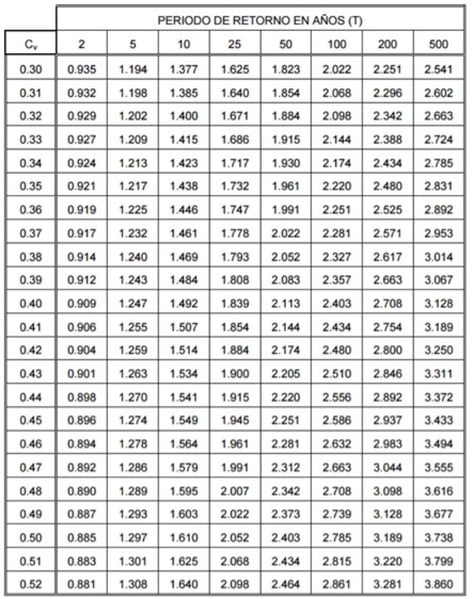
4.) Realizar el producto del factor de amplificación (KT) por el valor medio de la máxima precipitación diaria anual en milímetros (Pt), obteniendo la precipitación diaria media máxima para el periodo de retorno deseado (Pd). El dato (Pt) se puede consultar en diferentes estaciones meteorológicas.
![]()
Una vez establecido lo anterior, el primer parámetro que se debe obtener es Intensidad de las lluvias (It) para el tiempo de concentración calculado, mediante la siguiente fórmula:
![]()
Donde:
- I(T,t): es la intensidad de precipitación de cálculo.
- Id: es la intensidad media diaria correspondiente a un período de retorno T en mm/h.
- Fint: es el factor de intensidad.
Para el cálculo de Id se tendrá en cuenta la precipitación diaria Pd calculada anteriormente, que se relacionan mediante la fórmula:
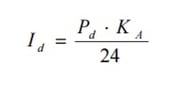
Donde KA es el factor reductor de la precipitación, cuyo valor se obtiene a través de la siguiente expresión, introduciendo el área (A) en km:

Para el cálculo del factor de intensidad hay que tener en cuenta que depende del periodo de retorno (T) y de la duración del aguacero en horas (t). Su valor será el mayor de los dos siguientes: Fa o Fb.
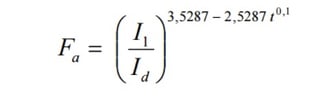
Donde:
- t: es el tiempo de concentración que, para este parámetro, debe particularizarse como el valor del tiempo de concentración (t=Tc).
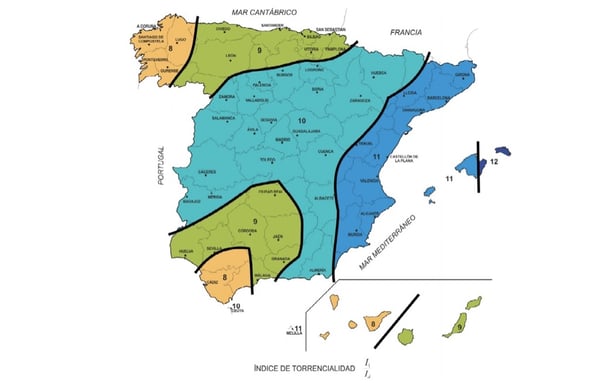
- I1/Id: se recoge del mapa de valores I1/Id para España, que se muestra a continuación:
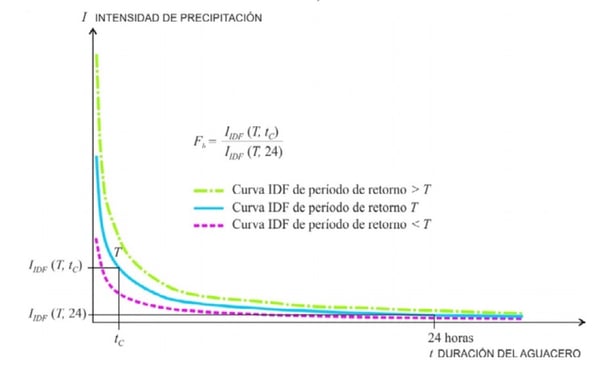
En el caso de Fb, su valor se obtiene a partir de las curvas IDF de un pluviógrafo próximo, a partir de la ecuación:
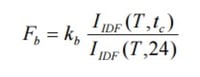
Donde:
- Kb: es un factor que tiene en cuenta la relación entre la intensidad máxima anual en un período de veinticuatro horas y la intensidad máxima anual diaria. En defecto de un cálculo específico se puede tomar kb = 1,13.
- IIDF (T,tc): es la intensidad de precipitación correspondiente al período de retorno T y al tiempo de concentración tc, obtenido a través de las curvas IDF del pluviógrafo.
- IIDF (T,24): es la Intensidad de precipitación correspondiente al período de retorno T y a un tiempo de aguacero igual a veinticuatro horas (t = 24 h), obtenido a través de curvas IDF siguientes.
Con esto, ya se habría obtenido el primero de los parámetros de la fórmula del caudal máximo.
El segundo paso será calcular el valor del Coeficiente de escorrentía (C) (relación entre la parte de la precipitación que circula superficialmente y la precipitación total), aplicando la expresión siguiente:

Donde:
- C: Coeficiente de escorrentía.
- Pd: Precipitación diaria media máxima para el tiempo de retorno establecido (mm).
- KA: es el factor reductor de la precipitación.
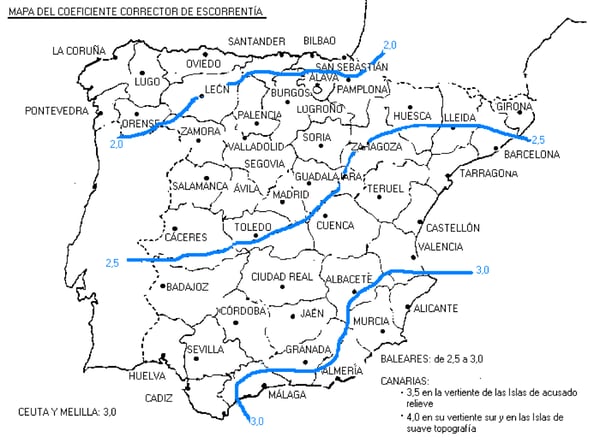
- P0 = umbral de escorrentía corregido en mm. Esta magnitud se define como precipitación mínima que debe caer sobre la cuenca para que se inicie la generación de escorrentía. El valor del umbral inicial puede obtenerse de los datos y mapas publicados por la Dirección General de Carreteras. Su corrección vendrá dada por la multiplicación de su valor inicial por un coeficiente β, cuyo valor se obtiene a partir de una serie de expresiones que vienen definidas en la nueva norma.
Como una aproximación suficientemente correcta de este último coeficiente corrector, se presenta el valor que se obtenía a raíz de la anterior Instrucción. Aunque se advierte aquí que para obtener un valor más real deberá acudirse a la Instrucción nueva.
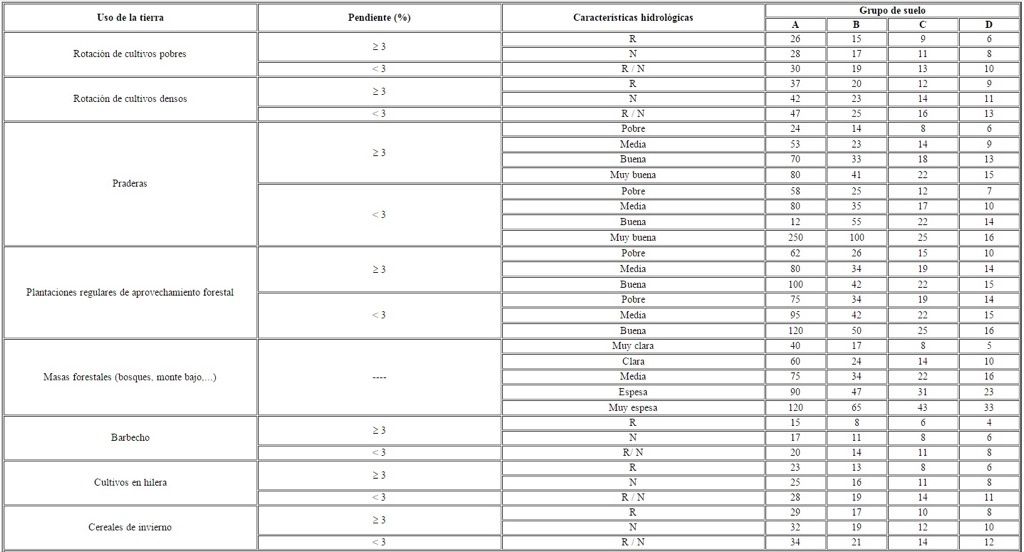
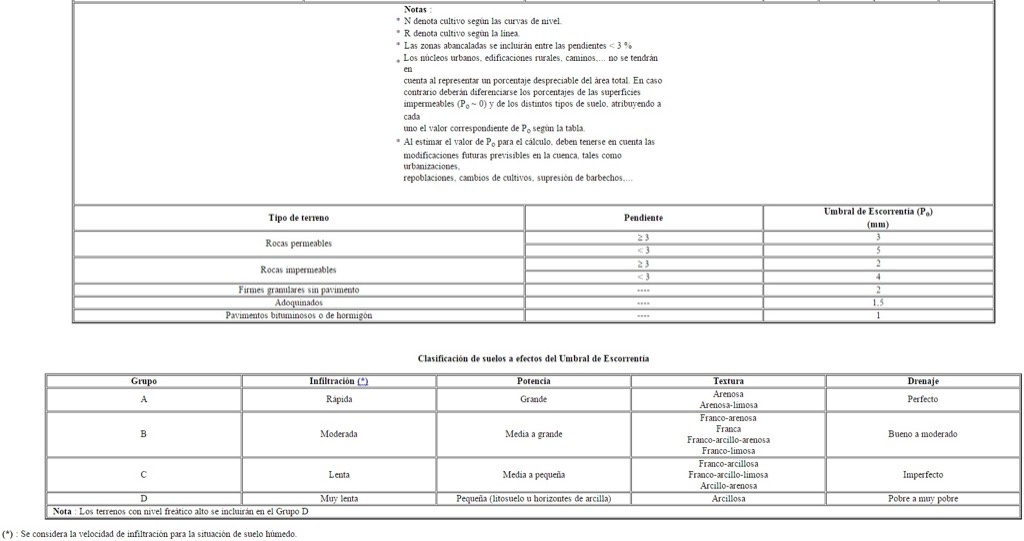
El valor de P0 se suele estimar, aunque existe un método para su obtención recogido en la nueva Instrucción, teniendo en cuenta que éste dependerá del tipo de suelo y de su vegetación. Para ello, existen unas tablas en las que se debe entrar teniendo en cuenta lo anterior:
El tercer paso que se debe realizar para conocer el caudal de avenida es obtener el valor de la superficie de la cuenca en km (A) que, a los efectos de esta norma, se considera como la superficie medida en proyección horizontal (planta) que drena al punto de desagüeque aportará caudal al proyecto de estudio.
Por último, faltaría conocer el valor del factor de uniformidad (K). Se obtendrá a partir de la siguiente ecuación, teniendo en cuenta que se debe introducir el tiempo de concentración en horas:
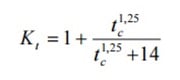
Con todo lo anterior, se habrán obtenido todos los valores de las distintas variables de las que depende el caudal máximo, con el que se podrán diseñar los drenajes de nuestras obras, tal y como se describió al inicio de este texto, mediante la siguiente fórmula:
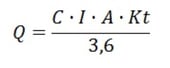
Si quieres saber más sobre el cálculo de drenajes, puedes consultar nuestro posgrado:
Máster en Construcción, Mantenimiento y Explotación de carreteras
Drenaje Superficial, Longitudinal y Transversal en Obras Lineales






