Proyecto TFM: Modelo para la detección de fraudes en transacciones

Los ciberataques están a la orden del día. ¿Eres capaz de crear un modelo para detectarlos? Este interesante TFM lo ha logrado.

Actualmente, con el avance de la tecnología y el acceso a Internet, los pagos han evolucionado y existen diferentes formas de realizarlos, ya sea de manera física o virtual. Así como los pagos han ido cambiando para adaptarse a las necesidades y comodidades de clientes y comercios, los ciberdelincuentes también han ido evolucionando. A pesar de las diferentes medidas de seguridad que adoptan las entidades financieras, los fraudes en medios de pagos es una problemática que se enfrenta día con día.

Las entidades financieras y emisores de medios de pago deben evolucionar en conjunto con las necesidades del sector, hacer uso de la creciente tecnología y la disposición de datos para establecer medidas de seguridad y establecer medidas de detención temprana de fraudes.

Creación de modelo para la detección de fraudes en transacciones en tarjetas de crédito

Este interesante TFM elaborado Magaly Fonseca ex-alumna del Máster en Big Data y Business Analytics en Structuralia nos profundiza en esta temática tan importante hoy creando un "Modelo para la detección de fraudes en transacciones de tarjetas de crédito". 

1. Elección de Dataset

Para la elaboración de este trabajo de fin de master se seleccionó un dataset, de los disponibles en la página Kaggle, el cual cuenta con información para trabajar con el objetivo de entrenar un modelo de aprendizaje capaz de detectar casos de fraudes en las transacciones. El dataset elegido se llama card_transdata el cual contiene información de transacciones con tarjetas de crédito.

El dataset es un archivo de extensión csv y consta de 8 columnas. Descritas a continuación:

• Distance_from_home: la distancia desde casa respecto a donde ocurrió la transacción.

• Distance_from_last_transaction: indica la distancia entre el punto de la transacción con respecto a la última transacción registrada, es decir, la transacción anterior.

• Radio_to_median_purchase_price: es la relación entre el monto de la transacción y el precio medio de compra del cliente.

• Repeat_retailer: indica con 1 si la transacción se realizó desde el mismo minorista y con 0 si no.

• Used_chip: en esta columna se indica con 1 si en la transacción se utilizó el chip de la tarjeta de crédito y con 0 si no se utilizó.

• Used_pin_number: en este campo se señala con 1 si en la transacción se usó el número de pin y con 0 en caso contrario.

• Online_order: se indica con 1 si la transacción corresponde a un pedido en línea y 0 si no fue así.

• Fraud: indica si la transacción fue identificada como fraude o no, al igual que las columnas anteriores con los valores 1 para los casos fraude y 0 para los no fraude.

2. ETL con Trifacta

Para el proceso de extracción, tratamiento y carga de los datos (ETL) se hace uso de la herramienta Trifacta. Para iniciar el proceso se carga el dataset card_transdata.csv en la herramienta y se crea el flujo con el nombre de “datos de transacciones”.

Como primer paso en el proceso de transformación se realiza el perfilado de datos, con el fin de conocer a fondo el contenido del dataset y verificar la calidad de los datos con el objetivo de determinar las transformaciones que deban realizarse para poder trabajar con los datos y obtener resultados confiables.

Imagen 1. Verificación de la calidad de los datos iniciales en Trifacta.

Según se muestra en la imagen anterior, los datos de las 8 columnas del dataset se encuentran con una buena calidad ya que la barra indicadora en todos los casos se encuentra en verde, lo que se traduce en que los datos están correctos, coinciden con el formato de la celda y no hay valores inválidos ni vacíos. Se puede apreciar además que el dataset tiene dos tipos de datos: enteros y decimales. Por lo tanto, se procede a finalizar el proceso de ETL, corriendo el job en Trifacta para obtener el dataset y continuar con la parte analítica del mismo.

Parte importante al trabajar con datos es conocerlos y realizar un estudio analítico que nos permita tomar las mejores decisiones para el tratamiento de los mismo, para dicho proceso se realizó el análisis en Python.

1. Análisis EDA

Imagen 2. Gráficos de las variables categóricas.

Gracias a los gráficos se puede observar que el 88.2% de las transacciones se realizaron en el mismo minorista que la compra anterior. En el 35% de las transacciones se utilizó el chip. En el 10.1% de las compras se usó el pin y el 65.1% de las transacciones fueron compras en línea. Por último, el 8.7% de las transacciones son fraude.

Se realizan boxplot para las variables continuas, para observar la distribución de los datos de dichas variables:

Imagen 3. Boxplot de las variables continuas.

En las tres variables se pueden observar que existen valores atípicos que sobresalen del resto de datos, al considerar la descripción de las variables, a saber: distancia desde casa, distancia desde la última transacción y razón respecto a la media de compra; además tomando en cuenta que lo que se desea más adelante es entrenar un modelo que prediga si la transacción corresponde o no a un fraude, estos valores atípicos podrían representar movimientos de fraude por lo que se determina que deben mantenerse.

2. Estudio de correlaciones

Parte importante del análisis es realizar un estudio de correlaciones para observar si existe relación entre las diferentes variables que componen el dataset. Debido a que se tiene variables continuas y categóricas se utiliza el método de Spearman, que se puede utilizar para ambos tipos de variables:

Imagen 4. Correlación de las variables

En el resultado se puede apreciar una fuerte correlación (0.6) entre las variables distancia desde casa y si la compra se realizó en el mismo minorista. Además, se puede apreciar un adelanto de las variables que influyen en la variable de nuestro interés (fraude) donde la razón respecto a la media de compra es la variable que tiene mayor correlación con fraude (0.3) aunque el valor no es tan alto, le sigue la variable compra en línea con 0.2 y distancia desde casa con 0.1. Un punto importante resalta de este análisis, aparecen dos variables con correlación negativa con fraude, las cuales son uso de chip y uso de número de pin ambas con un valor de -0.1 lo que se podría interpretar que el uso de esto dos métodos de seguridad son efectivos para evitar el fraude en las transacciones.

Como último paso del análisis estadístico se realizan pruebas de hipótesis (anova) para corroborar la influencia o no de las variables en nuestra variable de interés que es el fraude, se muestra el resultado:

Imagen 5. Resultado de Anovas

Como se puede apreciar, la única variable que tiene un valor mayor a 0.05 es si la compra fue en el mismo minorista, por lo que se rechaza la hipótesis nula de que la variable es influyente. El resto de variables sí son influyentes.

4. Visualización

Una vez realizado el proceso de ETL y el análisis estadístico de los datos disponibles, se procede a cargar el dataset en PowerBI para la creación de un dashboard que permita visualizar la información disponible:

Imagen 6. Carga del dataset a PowerBI.

Una vez cargada el dataset, se procede a realizar algunas transformaciones de los datos, solamente para facilitar la visualización, dichas transformaciones corresponden al tipo de dato de las columnas con información booleana, se pasa de 0 y 1 a tipo “true/false” y en el caso de la columna Fraude se cambia el tipo de dato a texto y se reemplazan los 0 por la palabra “no” y los 1 por “si”. Cabe indicar que estas transformaciones se realizan solamente para efectos de facilitar la visualización, pero no modifican la fuente de los datos (el dataset).

Con las transformaciones descritas anteriormente, se procede a crear el dashboard con la información relevante para el caso en estudio:

En el dashboard se puede visualizar como dato principal la cantidad total de fraudes detectados, que corresponde a 87403 casos; lo cual representa el 8.74% de las transacciones, fácilmente observable en el gráfico de pastel.

Además, se muestra una tabla en la que se compara las medianas de las variables numéricas para los casos fraude respecto a los no fraude, en dicha tabla se puede apreciar una diferencia significativa en las medianas de la variable “razón respecto a la media de compra” en los casos de fraude (5.07) en comparación a las transacciones no fraudulentas (0.91); también existe una diferencia importante en las medianas de la variable “distancia desde casa”, ya que en los casos de fraude la mediana es mucho mayor que los casos de no fraude; mientras que para la variable “distancia desde la última transacción” la diferencia de las medianas no es significativa (0.2).

Por último, se muestran 4 gráficos de barra, uno para cada variable booleana relacionadas a la variable fraude. Se puede observar fácilmente en ellos que para los casos de fraude la mayoría de las transacciones se realizaron en el mismo minorista, también se aprecia que la mayor proporción de fraudes se realizaron en compras en línea. Además, se puede apreciar que las medidas de seguridad como el uso del chip y el número de pin son efectivas para la prevención de fraudes, siendo el uso de numero de pin más efectiva.

5. Construcción de modelo de detección de fraudes

Con el objetivo de realizar un modelo de detección de fraudes, lo cual sería un modelo de aprendizaje de clasificación. En primera instancia se procede a determinar las variables a utilizar, como se determinó al final del análisis estadístico, las variables que son influyentes para determinar si es fraude o no son todas excepto si la compra fue en el mismo minorista. Además, esta variable tenía una alta correlación con la variable distancia desde casa, por lo que solamente se debe utilizar una de ellas, esto representa una razón mas para descartar la variable “repeat_retailer”.

1. Definición de variables de entrada y salida.

Con la información anterior, se procede a definir las variables de entrada y salida como primer paso de la construcción del modelo; se define también los datos de entrenamiento y prueba, siendo de prueba el 30% de los datos; además, se realiza un escalado de los datos.

Una vez definido, se procede a realizar la predicción utilizando diferentes métodos de aprendizaje supervisado.

2. Árbol de decisión

Se realiza una matriz de confusión para verificar la calidad del modelo

Resultado de la matriz de confusión:

Según lo mostrado en la matriz de confusión se procede a calcular las métricas que nos indiquen la calidad del modelo. Tenemos lo siguiente:

TP = 273905

FP = 2

FN = 2

TN = 26091

Accuracy = 0.9999

Se aprecia un accuracy muy bueno; sin embargo, como se apreció en el análisis estadístico los casos de fraude corresponde a un 8.7% de los datos, por lo que se tienen los datos desbalanceados, es decir, se tiene muchos datos de una clase (no fraude) y pocos de otra (fraude). Dado lo anterior, se procede a calcular el F1 score, la cual es la métrica más adecuada para este tipo de casos.

Precision = 0.9999

Recall = 0.9999

F1 score = 0.9999

Se puede apreciar que el F1 score es muy cercano a 1 por lo que se puede concluir que el modelo tiene muy buena calidad y tendrá mucha efectividad al predecir próximas transacciones fraudulentas.

3. Random Forest

Se muestra el resultado de la matriz de confusión.

Como se puede apreciar tiene el mismo resultado que con el árbol de decisión.

4. K-nearest neighbors

Resultado de la matriz de confusión.

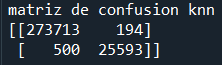
Con la matriz anterior se puede apreciar que la calidad de este modelo es menor que la del modelo con el método de árbol de decisión. Se calculan las métricas de evaluación del modelo:

TP = 273713

FP = 194

FN = 500

TN = 25593

Accuracy = 0.9977

Precision = 0.9993

Recall = 0.9982

F1 score = 0.9987

5. Naive bayes

Resultado de la matriz de confusión:

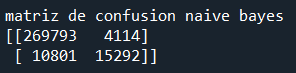
Se puede observar que con este método la calidad del modelo decae aún más en comparación con los modelos anteriores. Se muestran las métricas de evaluación:

TP = 269793

FP = 4114

FN = 10801

TN = 15292

Accuracy = 0.9503

Precision = 0.9850

Recall = 0.9615

F1 score = 0.9731

 6. Comparación de los modelos

Finalmente, a modo de resumen se muestra una tabla comparativa de las métricas de los diferentes modelos utilizados, donde se puede apreciar que el método con mejor métricas y por tanto el que debe usarse es el árbol de decisión con un F1 score de 99.99%

7. Clustering

Otra parte importante para el negocio es categorizar las transacciones, haciendo uso de las ventajas que brinda el machine learning y data mining se procede a realizar el clustering. Para este objetivo se trabajó con las variables numéricas disponibles en el dataset. Como se pudo apreciar en la visualización (dashboard de PowerBI), las variables “distancia desde casa” y “razón respecto a la media de compra” fueron las variables que presentaron mayor variación en las medianas cuando se analizaban por separado los casos fraude respecto a los que no son fraude; es por esta razón que se toman estas dos variables para el proceso de Clustering.

Para determinar la cantidad idónea de cluster se utiliza el método Elbow.

A continuación, se muestran los resultados de dicho método, como se puede apreciar la cantidad de cluster a usar es 3.

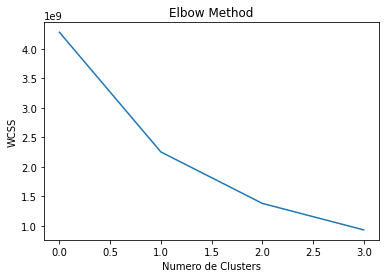
Imagen 8. WCSS en función de K (número de clusters).

Una vez definida la cantidad óptima de clusters, se procede a realizar el clustering y a graficar para apreciar la distribución de los datos en cada uno de los clusters:

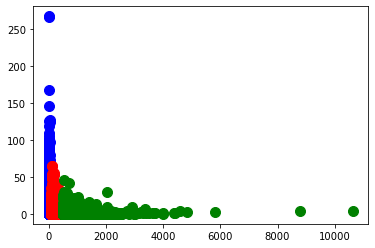En el gráfico se puede apreciar un primer cluster (azul) con transacciones que están cerca de casa pero con razón respecto a la media de compra alta. Además, un segundo cluster (rojo) con transacciones que tienen una distancia desde casa media y la razón respecto a la media de compra también media. Por último, un tercer cluster (verde) con razón respecto a la media de compra baja y distancia desde casa alta.

8. Conclusiones

• El dataset card_transdata tiene una buena calidad de los datos en su fuente original por lo que el tratamiento para los procesos posteriores es mínimo.

• El 8.7% de las transacciones en estudio corresponde a fraudes.

• Producto del estudio estadístico, se determina que las variables “distancia desde casa” y “mismo minorista” tienen correlación.

• Con respecto a fraude, se determinó que todas las variables del dataset son influyentes excepto la variable “mismo minorista”.

• En el estudio de correlaciones se aprecia cómo las medidas de seguridad adoptadas como uso de chip y uso de número de pin son efectivas para evitar el fraude ya que tienen una correlación negativa con los casos fraude.

• Se realizan diferentes modelos haciendo uso métodos de aprendizaje supervisado con el fin de detectar casos de fraude, siendo el más efectivo el modelo que utiliza el método árbol de decisión, con un F1 score de 99.99%, por lo tanto, es el modelo que se debe utilizar.

• Se realizó la categorización de las transacciones en 3 clusters, utilizando las variables continuas “distancia desde casa y “razón respecto a la media de compra”, haciendo uso del método elbow para determinar la cantidad óptima de cluster y utilizando el algoritmo K-Means para el clustering en sí.

El equipo de Structuralia agradece a Magaly Fonseca por su excelente trabajo realizado. ¡Mucho éxito en su carrera profesional y en todos los desafíos que se proponga por delante!